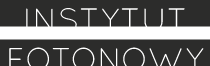You may have heard that quantum world is weird or even worse, that quantum mechanics (QM) is so unnatural that no one really understands it. Well, judge for yourself. If you read this note through and still think it’s all magic, punish yourself by buying from our competition.

The most abused example of inner workings of QM is the Schrödinger’s cat “paradox”. The idea is to magnify a small quantum object to a size of a big animal in order to demonstrate how strangely it behaves. The setup is the following: A radioactive atom is placed in a box with an alive cat. If the atom decays, this is what radioactive atoms do from time to time, the cat dies. If it doesn’t decay, the cat survives.

Applying rules of QM to the atom and the cat shows that after a while the atom is in, so called, superposition: decayed and not decayed, at the same time. So is the cat in superposition: of dead and alive.

The superposition means that if you had, say, 1000 identically prepared radioactive atoms and you check whether they decayed or not, you would find out that some of them did decay, some did not, while the rest could not be decided either way. If similar reasoning is applied to, say, 1000 cats the same fraction of animals should have been dead, alive or undecided.

There is this problem, though. No one have ever seen an “undecided” cat, i.e. both dead and alive.

On the other hand, there is no reason why the rules of QM should apply to an atom and not to cats that are built out of atoms, after all.

Does our everyday experience contradict the most tested theory of physics? If so, which is right? Aristotle used to say that contradictions do not exist.
Well, he is dead and right at the same time.

The solution to the puzzle is this: One can have undecided radioactive atoms. Cats consist of many atoms and each atom follows the rules of QM. Because, it takes so many atoms to form a cat, there are no undecided cats.

Here is a simple explanation.

One atom

Take a look at the upper plot of Fig. 1. It depicts possible outcomes of position measurement on an atom that had been prepared in a superposition of the left, centered around -1, and right state, centered around 2. If the atom happens to show up at position -2 it certainly came from the left state. If it was at position 3, the right state was the origin. The centers of the two states are separated by distance 3, which is larger than the width of the two states.

To have a chance of finding an “undecided” atom in the vicinity of the position 0.5, one would have to perform thousands of measurements on such atoms, one by one. Thus we can say that such an event is improbable.

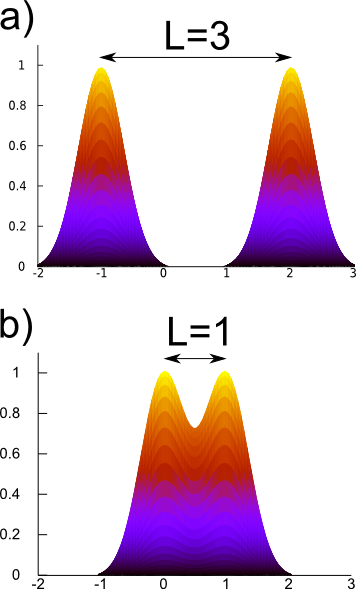
Fig. 1. a) An atom in superposition of two states: left and right. No undecided region. The atom found during measurement around -1 comes from the left state. The atom found around 2 comes from the right state. b) An atom in superposition of two states with large undecided region. One cannot tell whether the atom found around 1 came from the left or the right state.

A different picture is shown in the Fig. 1b. Here, an atom is in a superposition of overlapping left and right states. Thus finding it at the position, say 0, doesn’t reveal its origin. This is our model of an “undecided” atom.
I will use more atoms, all in the left state and all in the right state, at the same time, to model a Schrödinger’s cat.

Many atoms

In QM each additional atom brings a new dimension with it. If one atom is considered, its possible positions are depicted in the one dimensional plot of the Fig. 2a. Two atoms, both like the one in Fig. 2a. require two dimensional plot as in the Fig. 2b. Here the separation between states is more convincing. For three such atoms — three dimensional plot are in order, and so on. A typical cat consists of more than 1025 (or 10,000,000,000,000,000,000,000,000) atoms.

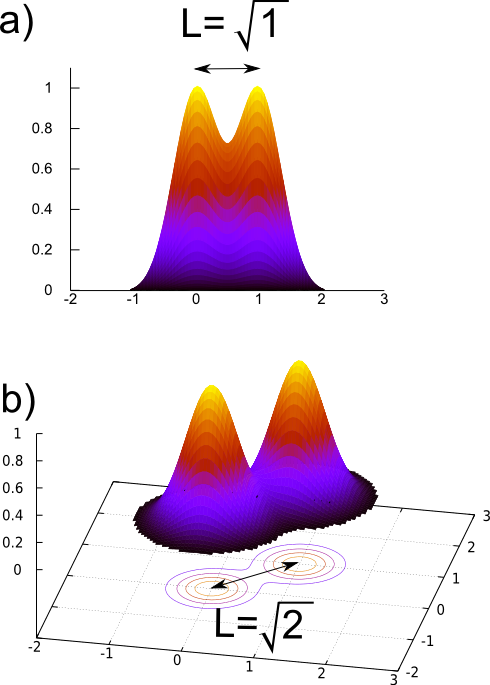
Fig. 2. a) One atom in the superposition of states left and right. b) Two identical atoms in superposition left and right.

Crucial observation

A single atom originates from the left or the right state centered at 0 and 1 positions, respectively. The width of the states is comparable with their distance in 1D, so the states overlap.

If we consider N atoms, the distance between left and right becomes √N, while their width remains unchanged. Thus, for the multi-atom cat: all atoms in the left and, simultaneously, all atoms in the right state, the corresponding multidimensional plot would consists of two perfectly well, by any experimental standards, separated parts. This is why, a measurement of a cat reveals the origin, the left (dead) or the right (alive) state, beyond any doubt.

One can say that there are no undecided cats for geometrical reasons. Shear dimensionality of the multi-atom space solves the paradox.

For professionals: Here I considered only a bosonic Schrödinger’s cat: superposition of two slightly displaced condensates. The argument for a fermionic one is the same. Even a tiny displacement of the center of mass (in 3D), corresponding to dead and alive cat, results in two completely separated multidimensional probability distributions.

Zbigniew Karkuszewski, February 22-nd 2009