The text bellow has been rejected by: Nature, Science, Physics Reports, Reviews of Modern Physics, Physical Review Letters and arXiv without even reaching a referee stage 🙂
Please, let me know if you have an idea how to extend the list above.
Although, quantum mechanics is the same for microscopic and macroscopic objects, there is a perception that the later do not exhibit basic quantum properties like superposition or interference. Historically this view has been encapsulated in a story called Schrödinger’s cat paradox, where a cat is, in full agreement with the rules of quantum mechanics, prepared in a superposition of two states: dead and alive. The paradoxical part is that no one has ever seen such a situation in the real world where large object would be simultaneously dead and alive or in two distinct places at the same time.
Here I show that there is no difference, in principle, between large and tiny objects. In fact, quantum features absent for large objects can be easily suppressed for microscopic objects as well. Moreover, I demonstrate that in transition from micro- to macro-world there is no need for any arbitrary quantum-classical border or any assistance from an external environment to resolve the paradox.
Introduction
Quantum mechanics (QM) is being developed for over 80 years, but one cannot say that the theory has matured by now. To the contrary, fundamental issues within quantum mechanics are still debated. What is the meaning of wave function – does it represent only ensembles or also individual objects? How to deal with the measurement process – should the measuring apparatus be classical or quantum? Is the measurement process part of quantum mechanics at all?
Even if the correct resolutions of those problems can be found in the literature, none of them are uniformly accepted by physicists.
In such circumstances, an argument that hopes to settle one of the great issues in QM in an easily reproducible way may be of interest to the scientific community.
In the following, a superposition of two spatial states will be considered rather than the dead and alive states. This choice comes with no harm to the generality of the solution, still it is simpler to quantify position of an object than vitality of an animal.
The well known Young double-slit experiment is one of the core examples of intrinsic workings of QM. It is also suitable for illustrating the resolution of the Schrödinger’s cat paradox.
A single photon “paradox”
Two slits, that are placed in the way of photons, produce an illumination pattern on a screen or a detector array. See Fig.1. Each photon passing the slits will leave a single dot on the screen. The relative position of slits and the screen affect the pattern.

Fig. 1.Young experiment setup with screen either close to the slits (t = 0.02) or far away from them (t = 2.2).
In particular, if the screen is close to the slits, two fringes will appear. The fringes are just projected images of the two slits, Fig.1. For each yellow point on the screen there is no doubt where the photon, that produced it, came from. The left fringe corresponds to the left slit, the right fringe to the right slit. If one blocks, say, the right slit, the left fringe will stay the same.
If the screen is far enough from the slits, many interference fringes appear and there is no way to determine the origin of any photon that has reached the screen. In fact, the presence of the interference fringes is a manifestation of that indeterminism. Any successful attempt to track the photons back to a slit would destroy the interference pattern. In both cases, screen close to the slits and far from them, the quantum state of the photon is a superposition of two possibilities: photon originated from the left slit and photon originated from the right slit. However, in the first case, one can tell from which slit did the photon emerge because the two superposing states are spatially separated, Fig.2 a).
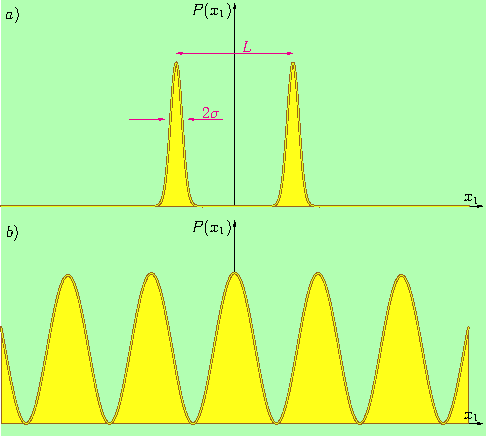
Fig. 2. Probability density along the dashed line in the screen of Fig.1 with screen a) close to the slits (t = 0.02) or b) far away from them (t = 2.2).
Therefore, if one formulated a single photon paradox in this fashion: Why don’t we see a superposition of a photon when the screen is close to the slits? After all, it has been prepared in the superposition of the left slit + right slit states. the answer is clear. We don’t see any superposition with a single photon because it leaves only one mark, in the left or the right fringe. It could happen that the mark will be left in the region between the fringes. In such case one may not be able to determine which slit the photon has passed through. It is, how- ever, less and less probable with the increasing L/σ ratio. We could infer about the superposition by repeating the single photon experiment many times and recording the two fringes that indicate the superposition (or mixture of states).
If, in the single photon paradox, we replace the word ”superposition” with ”interference” then the answer is that the two superposing states are spatially separated and there is no interference possible. One can firmly tell which slit the photon has originated from. There are only left-slit-photons and right-slit-photons and each mark on the screen belongs to one of the two. For the far away screen, we still will not see any superposition with just one photon, because a single spot on the screen does not reveal any. However, after many repetitions of the same experiment, we can learn that the interference pattern emerges, Fig.3 b). To prove that, one can block one of the slits and the interference fringes will not form.
To summarize, a single photon behaves similar to a hypothetical Schrödinger’s cat when the screen is close to the slits. Despite being described by a superposition of left-slit plus right-slit states it cannot show any signs of the superposition or interference. If experiment is repeated many times, only left-slit or right-slit photons are detected. Likewise, only alive or dead cat can be seen in the paradox. The similarity is explained in the next section.
Schrödinger’s cat state
There are many possible and equivalent versions of the Schrödinger’s cat state. The essential part is that they involve superposition of an object consisting of large number of quantum elements.
Within the setup of the Young experiment, one can produce such a state, too. It corresponds to the following arrangement: N photons passing through the left slit and no photons passing through the right slit plus no photons passing through the left slit and N photons passing through the right slit. N is of order of Avogadro number i.e. about 1024.
Symbolically, the Schrödinger’s cat state can be denoted as
(1) ![]()
where the left slot in the |…, …〉 ket stands for the left slit, later represented by a Gaussian centered in position −L/2, and the right slot for the right slit, later represented by a Gaussian centered in position L/2.
Conveniently, the state of a single photon considered in previous section has the same form but with N = 1.
Fringes appearing on the screen are completely determined by the state from Eq.(1). For N = 1 the probability density across the dashed brown line in plane of the screen in the Fig.1 has this form:
(2) ![]()
where x1 is a position variable along that line, L is the slits separation,σ≪L corresponds to the width of the slits and parameter t describes distance of the screen from the plane of the slits. The Eq.(2) has an interesting structure, it is a sum of three components. First two components describe the two fringes that are projections of the slits, the third one is an interference term. For example, if the distance of the screen from the slits is small i.e. t≪σ, the interference term is suppressed by the exponent with L2≫ σ2 and only two fringes remain, Fig.2 a).
On the other hand, for far away screen i.e. t/σ≫L the interference term dominates, Fig.2 b).
When more than one photon state is considered, there is a slight complication with the picture. Each photon brings an extra dimension to the probability density. For N photons the Eq.(2) turns into
(3) ![]()
where index j counts the photons. Despite the multidimensional character, the probability density has a similar structure to that of one-photon state: the first two terms in the sum correspond to the projection of the slits on the N-dimensional space span by x1, …, xN variables and the third term is an interference component. The multidimensional analysis of the Eq.(3), even for N ∼ 1024, is quite straightforward. The interference term is suppressed even faster than before due to the N factor in the exponent with L2. The two remaining multivariate Gaussians have radius√(σ2 + (t/σ)2) and centers at (x1 = −L/2, …, xN = −L/2) i (x1 = L/2, …, xN = L/2).
The geometric distance of the centers is L√N, which is a large number as compared to the radius for moderate values of t. Thus, the two components of the probability density are spatially separated due to the large number of photons comprised by the Schrödinger’s cat.
Another way of inspecting the probability density is to use its one-dimensional cross section
x/√N = x1 = … = xN along the line that connects the centers of the two multivariate Gaussians i.e. passing through points (x1 = −L/2, …, xN = −L/2) i (x1 = L/2, …, xN = L/2)
(4) ![]()
The cross section shows that large N will supress the interference term and expand the distance of the remaining Gaussians by factor √N. Again, the two Gaussians will be spatially separated for moderate values of t. That, in turn, implies that even if the screen is far away from the slits there will be neither interference pattern nor any ambiguity as to where each cat came from, the left or the right slit. All the events that are somewhere in the middle of the two Gaussians are highly improbable.
Conclusions
By varying N in (2) i (3) from 1 to 1024 one can explore the transition from micro- to macro-world all in terms of the Young experiment. The spatial separation of the multivariate Gaussians in the probability density goes from L to 1012L. Therefore, in macroscopic case, an experiment with one cat will necessarily reveal the cat passing through the left or the right slit.
The transition is smooth an has no place for the quantum-classical border. In fact, the end result for the Schrödinger’s cat state is very similar to the single photon state with the screen close to the slits. The lack of superposition and interference has exactly the same explanation in the two cases. One can say, that the Schrödinger’s cat state is as mysterious as a single photon state with the screen close to the slits.
Schrödinger’s cat versus photon (pdf)
Zbigniew Karkuszewski, December 19-th 2013